前言

之前在 b 站上刷到了影视飓风的 “扫雷，但是是真人3D版！” 这个视频，总之很有感觉！

开始想着能不能直接用 UE5 复现一个，不过自己也没有那个能力，但是对扫雷的地图生成算法产生了一些兴趣。高中的时候经常和同学在 seewo 上面多开扫雷，当扫雷地图大了之后总遇到需要猜的死局，虽然后来在网上找到了一个可以生成绝对有解地图的扫雷，不过当时并没有想明白原理，正好这次尝试一下。

扫雷基本定义与规则

游戏初始局面为一块 \(n\times m\) 的矩阵，每一格都是未知的，玩家可以点击打开格子，若格子下是雷则游戏结束（一般保证第一次点击不是雷），否则格子下会出现一个数字，代表此格周围 \(8\) 格中的地雷数。若周围没有雷则会递归打开周围的 \(8\) 个格子。

而因为机制问题，有时候会出现因为条件不够需要猜测的局面。针对此衍生出了几种不同的玩法，详见下图（Source）：

扫雷分类

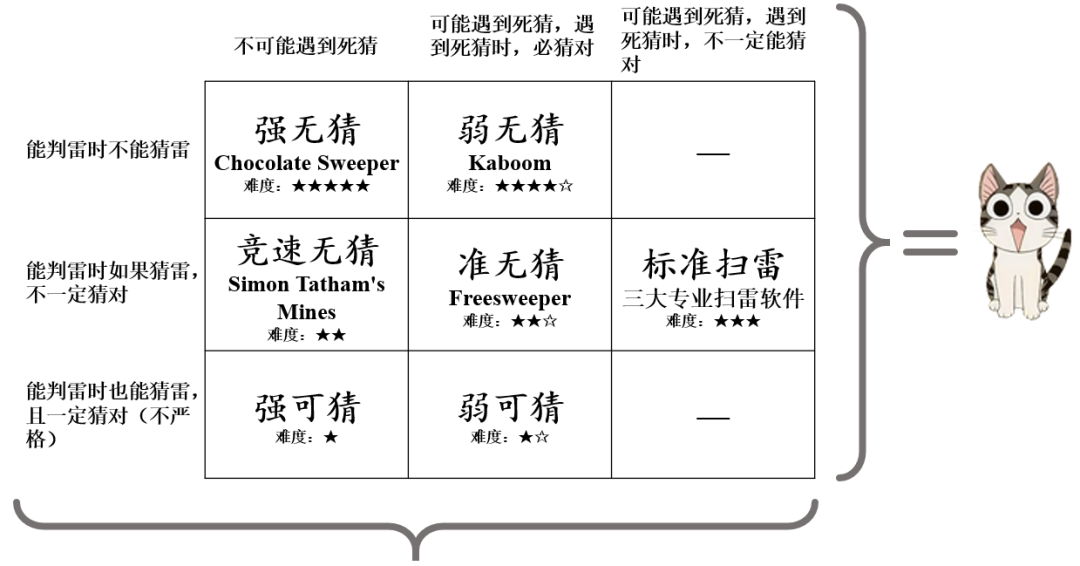
部分玩法的在线试玩：

扫雷问题求解

先来看看如何对指定的局面进行求解。

首先需要明确的是，扫雷的求解是一个 NP-Complete 问题（证明），意味着并没有多项式时间复杂度的解法。

将问题简单化，先思考怎么对一个局面在已知条件下解开至少一个格子，然后对局面不断求解就可以得到最终答案。

假设目前局面相关的格子数量为 \(O(n)\) 的，那么考虑一下怎么得到一个 \(O(2^n)\) 左右的算法？

（什么是局面相关的格子？举个例子，下图中受周围数字条件制约的，即可能解出来的格子。图示扫雷 Source）

ms1

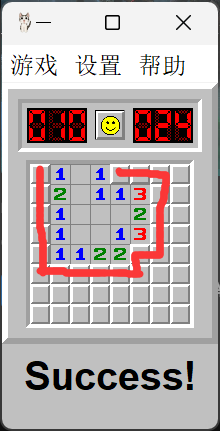
最简单暴力的想法就是直接 \(O(2^n)\) 的枚举所有的可能，代进去判断是否可行。若有多种可能就是遇到了需要猜测的情况。

可以优化吗？在搜索的时候可以简单判断一下，如果雷数已经超出了周围的限制或者无论如何也无法达到，就可以进行剪枝。（对于猜雷一定猜对的玩法，可以遇到一组合法解就直接退出）

此外，一个数字针对周围格子的限制可以用一个方程表示，即 \(x_1+\cdots+x_n=a\)，问题就转化成了给定一个方程组，求 \(0\)、\(1\) 整数解及数量。

我起初有考虑过直接进行高斯消元，如果得到唯一解（线性无关方程数量大于等于未知数数量）就是答案，但是会发现对于方程组多解的情况无法判断，在这无数组解中无法判断有多少 \(0\)、\(1\) 整数解，可能存在只有一组的情况，这样也是合法的。

但是可以在进行 \(O(2^n)\) 搜索前先进行一次 \(O(n^3)\) 的高斯消元（相比搜索复杂度影响不大），若能解出一部分变量的值就可以先解开一部分格子。

其次，对于 \(n\) 个未知数 \(m\) 个线性无关方程的高斯消元，我们知道可以由 \(n - m\) 个自由元的取值确定整个方程组的解，那么在搜索前可以先求出自由元，期望下可以大量减少可能性。

在此基础上，对于无法确定的格子，通过枚举所有可能性还可以计算出是雷的概率（需要考虑是否知道局面上剩下的雷数量并进行计算）。

而对于局面上有多个连通块的情况，可以将无关的连通块分开计算，这样也可以大大降低所需时间，对于概率计算就可以将不同的连通块组合在一起（类似一个背包 DP）

扫雷地图生成

其实我更感兴趣的是如何生成只有唯一解的扫雷地图。但是在网上查了查并没有发现任何的资料，似乎都是随机生成的。

于是直接套上面的求解算法，不断随机生成地图判断是否有解。

想了想怎么优化，不过除了多线程暂时想不出来其他方法，试了试如果在地图 \(20\times 20\)，雷密度 \(15\%\) 的情况下还是很快的。

碎碎念

实现了部分算法，放在 Github 上了。

没有进行专门的测试，因此大概率有 Bug

一个 1k 行的东西摸了一个多月。。感觉没救了

写的时候尝试了一下工程的感觉？虽然我也不知道工程什么样的，按着 Google-CPP-StyleGuide 写了下来。

在想能不能做个多人联机扫雷？像是合作 / PVP 等，甚至还可以结合迷宫做过恐怖游戏，不过 UE 已经忘干净了。